Cryptography hash method MD4 (Message Digest 4) explained with Python

Stuart Lippincott — https://www.behance.net/gallery/44523987/October-Everyday-Project

In the continuity of my previous article on the algorithm MD2 (available here: https://nickthecrypt.medium.com/cryptography-hash-method-md2-message-digest-2-step-by-step-explanation-made-easy-with-python-10faa2e35e85) my intent creating this serie is to popularize the algorithms of famous hash functions.

MD2, … MD4 !

This time we are going to look at the MD4 algorithm, if those are new to you I’d recommend you have a look at the MD2 article first as the MD4 piles up some additional complexity. Again I will go step by step through the full process implementing it using Python as we progress.

For the most perspicacious of yours, you’ll see a missing one here: MD3, if you explore the web looking for it chances are that you won’t find it. Presumably because it was never released and served more as a draft version of MD4, MD5 … but if you have any further information about it please feel free to share that with me: nick@thecrypt.io

The intent of the code is meant for functional usage but just for learning purpose, so there is a high chance that it will be sub-optimum and with potential memory flaws that could consist in security issues. Hence I would not recommend using this code expecting functional results.

That being said, let’s jump into the RFC 1320 (available here for example: https://tools.ietf.org/html/rfc1320).

This time, I will use the following text admitted to be from Isaac Asimov:

The saddest aspect of life right now is that science gathers knowledge faster than society gathers wisdom.

MD4 algorithm

Following the documentation, it consists in 5 steps that are as follow:

1. Append Padding bits
2. Append Length
3. Initialize MD buffer
4. Process the message in 16-Word blocks
5. Output

Before we starts I guess it will be quite useful for an illustrated reminder of what we mention when we refer to bits, byte, word …

Refresher on data size & bit operations

Let me just put here a small refresher on bits, bytes, words and various bit operations so we all have the same base:

• Bits (that stands for binary digit: remember that so you can shine when dining with your in laws) is technically the smallest data portion then considered as a unit that can be either 1 or 0.
• Bytes stands for a consecutive sequence of 8 bits (commonly referred to as an octet), if when read as decimal can be 256 different positions (from 0 to 255)
• A Word is a consecutive sequence of 32 bits or 4 Bytes

And here few bitwise operations that I put here as a reminder (taken from there: https://wiki.python.org/moin/BitwiseOperators):

• x << y : returns x with the bits shifted to the left by y places (and new bits on the right-hand-side are zeros). This is the same as multiplying x by 2exp(y).
• x >> y : returns x with the bits shifted to the right by y places. This is the same as dividing x by 2exp(y).
• x & y : does a “bitwise and”. Each bit of the output is 1 if the corresponding bit of x AND of y is 1, otherwise it’s 0.
• x | y : does a “bitwise or”. Each bit of the output is 0 if the corresponding bit of x AND of y is 0, otherwise it’s 1.
• ~ x : returns the complement of x-the number you get by switching each 1 for a 0 and each 0 for a 1. This is the same as -x-1.
• x ^ y : does a “bitwise exclusive or”. Each bit of the output is the same as the corresponding bit in x if that bit in y is 0, and it’s the complement of the bit in x if that bit in y is 1.

For those of you who experimented a bit simple cryptographic algorithm (substitution, xor, vigenere…) and the previous tutorial on MD2 we need to change our mindset as here we’ll be talking bits and not bytes/octets. It has a significant impact as the treatment of each 512-bits blocks will involve bit operations and not bytes operations.

Below you’ll find a concrete example within the block processing step section, but i’ll close this part talking about an animal it’s common to meet when talking cryptographic: modulo-2^32 addition or addition of words.

As we will be treating each blocks in words, each 512 bits blocks will have 16 ‘elements’ of 32 bits. As we will be processing with additions, things could get messy and exceed the capacity of our elements (the capacity meaning the maximum value of 2³² or 4,294,967,296). We need in our algorithm to ensure words remains words and hence proceed with each addition adding a modulo 2³².

A last reminder for people struggling with modulo, keep the image of the clock in mind: a clock can’t exceed the value of 12: when you pass 13h (1pm) you go back to 1, in other words 13 % 12 (which as well refer to the rest of the division 13 / 12), i hope this image help you as it helps me if it confuse you more… sorry please forget it — it’s very personal :)

Text parsing

The text we are using to go through the hash method can be represented as below:

Table as a representation of our text from I. Asimov

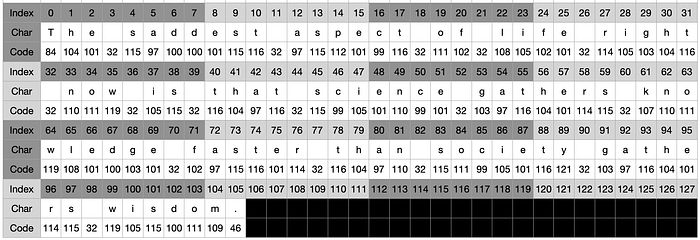
msg = 'The saddest aspect of life right now is that science gathers knowledge faster than society gathers wisdom.'

Then, as per our previous exploration of MD2 we would translate that table into a table containing the code of the characters stored as int:

msg = [ord(c) for c in msg]

MD4 step 1 — Append padding bits

This step is very straightforward, we extend the input message so its length in bits is congruent to 448 modulo 512. As put in the RFC we need to end up with a message which latest block’s length is 64 bits shy from 512 bits.

The padding pattern is as follow, a ‘1’ bit right after the message and then a serie of ‘0’ to reach 448 modulo 512.

Let’s design the padding bits, we will create a full 512 bits-block of padding (64 octets), which leads to an easier process: adding itto the message and then cropping the data element to its to the right length => 448 bits.

We will be working with bytes (1 octet, 8 bits, 1 character of the text phrase), the first serie of bits in the padding pattern is 1 then followed by zero, hence the first octet will be the one which matching ‘10000000’ (in binary)=> 0x80 (in hexadecimal) => 128 (in decimal)

Our padding pattern will be set as the below array of 64 Bytes:

PADDING = [
128, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

In order to properly add our padding we will need to seek for the exact number of bits to add. To do so let’s first start from the length of our message (without padding of course at that stage): 106 chars .

So, 106 chars (or octets) would represent 106 * 8 = 848 bits. Remember we need it to be congruent with 448 mod 512. So small recap here:

• 848 / 512 ≈1.65 means we have one full block of 512 bits here and almost 65% of a block (≈333 bits)
• 848 % 512 = 336 bits the exact number of bits we fill inside the last block of 512.
• Following this we need to feel 448–336 = 112 bits with our padding (or 14 chars from our padding pattern)

Now, if we take the scenario where we have 127 chars (1016 bits), so 1 block of 512 bits and 504 bits in a second block. We need then to add 8 + 448 bits from our padding pattern.

Basically we have two scenarios here:

• last block is below 448 bits: we fill 448-len(last_block) bits from our padding pattern
• last block is over 448 bits: we fill 448+512-len(last_block) or 960-len(last_block) bits from our padding pattern

As we work in octet let process all of this in 64 blocks octets, python code below:

msglen = len(msg)
index = msglen % 64
if index < 56:
msg = msg + PADDING[0:(56-index)]
else:
msg = msg + PADDING[0:(120-index)]

In our case, we needed 112 bits from our padding pattern as fillers or 14 characters, 1 x 128 and 13 x 0. If you print msg you will end up with the following array:

[84, 104, 101, 32, 115, 97, 100, 100, 101, 115, 116, 32, 97, 115, 112, 101, 99, 116, 32, 111, 102, 32, 108, 105, 102, 101, 32, 114, 105, 103, 104, 116, 32, 110, 111, 119, 32, 105, 115, 32, 116, 104, 97, 116, 32, 115, 99, 105, 101, 110, 99, 101, 32, 103, 97, 116, 104, 101, 114, 115, 32, 107, 110, 111, 119, 108, 101, 100, 103, 101, 32, 102, 97, 115, 116, 101, 114, 32, 116, 104, 97, 110, 32, 115, 111, 99, 105, 101, 116, 121, 32, 103, 97, 116, 104, 101, 114, 115, 32, 119, 105, 115, 100, 111, 109, 46, 128, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Which is exactly what we look for, let’s move on to the next step.

MD4 step 2— Append length of the message

At this stage we are still not in the hash process per se but formatting the input message. Now we will fill the remaining 64 bits of the last block that will help us reach a perfect size of 512 bits by blocks for our input message.

Here we will append to our processed input message a representation of the length of the message before padding, in the actual case i’m referring to our 106 characters of Asimov’s phrase.

Which is 106 bytes* 8 = 848 bits, so ‘848’ will be the value we will append at the end of the message within a 64 bits representation.

‘848’ translated into its binary form is 00000011 01010000, here it’s in two bytes as it’s superior as 256 (1 byte). But following the convention of the RFC we will work on the basis of the little endian, meaning we will start with the low order byte first.

In our case our 64 bits will then translate into this:

Length of the Asimov message ‘848’ bits under a 64 bit representation closing last block

As a consequence the last 64 bits (or 8 bytes) will be as below:

length_padding = [0x50, 0x03, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]

From a coding perspective it will be as simple as below:

msg = msg+list((msglen*8).to_bytes(8, 'little'))

There is a limit to this as you can imagine, in that case it’s if the length of the message in bits is over 2⁶⁴ or over 2300 To. We won’t be covering for this in our implementation due to low likelihood of this to happen and for the sake of keeping it simple. The RFC cover for this keeping only the low order 8 first bytes if it goes over the 64 bytes representation.

MD4 step 3 — Initialize MD buffers

The message digest will be built incrementing 4 variables (of 4 bytes size each, 32 bits word) that will need first to be initialized with the below specific values:

word_A = 0x67452301
word_B = 0xefcdab89
word_C = 0x98badcfe
word_D = 0x10325476

‘Magic’ values:

• word A is initialized with 0x01, 0x23, 0x45, 0x67 reversed
• word B is (prolonging A) with 0x89, 0xAB, 0xCD, 0xEF reversed
• word C is reverting the above 0xFE, 0xDC, 0xBA, 0x98 reversed
• word D is (prolonging C) with 0x76, 0x54, 0x32, 0x10 reversed

MD4 step 4— process each 512 bits block

In order to proceed, we will first define some auxiliary functions that will support the below computing operations.

The three following function takes 3 words as input and with some binary operations return 1 word.

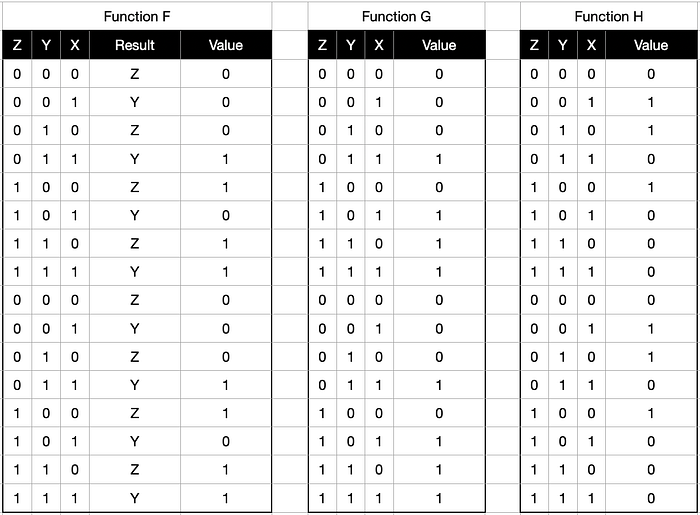
def fun_F(x, y, z):
return (((x) & (y)) | ((~x) & (z)))
def fun_G(x, y, z):
return (((x) & (y)) | ((x) & (z)) | ((y) & (z)))
def fun_H(x, y, z):
return ((x) ^ (y) ^ (z))

In brief, the functions acts as below bitwise operators:

• F: if X then Y else Z
• G: if at least two of X, Y, Z then ‘1’ else ‘0’
• H: X xor Y xor Z

Boolean table of the above, which will be applied to each bits of the words coming as input:

boolean tables of the algorithm auxiliary functions

We need as well to add a n-bit rotation, as defined below:

def fun_rotleft(x, n):
return (((x) << (n)) | ((x) >> (32-(n))))

The above consist in a standard circular-shift implementation, example on the initial value of word A with a rank 7 circular shift:

Example of the 7 circular-shift left-rotation on initial word A value

Remember each words addition will be made keeping it as a word, meaning we are keeping the result within 32 bits. To do so we will be applying % 2³² to each addition. From a code standpoint this will be as simple as ‘moduling’ the result with % 0x100000000. Everything over 11111111 11111111 11111111 11111111, or 4294967295 in decimal will be back to 0.

We are now ready to process each 512 bits block now.

First and foremost we will parse each 512 bits (64 characters) into a 16 words array, to proceed with our computing. In order to do so we will take each range of 4 characters (or 4 bytes) into an integer representation. I’m using the below function:

def decode_block(raw):
processdblock = []
for i in range(0, len(raw), 4):
proecssdblock.append((raw[i]) | ((raw[i+1]) << 8) | ((raw[i+2]) << 16) | ((raw[i+3]) << 24))
return(processdblock)

Example using our Asimov phrase, and its first 4 characters (consisting in the first word from our 16 elements block).

Parsing the first 512 block of the Asimov phrase into an array of words

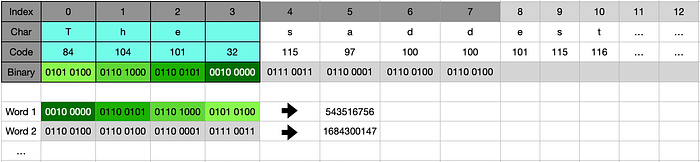
For each block, having our 16 word array we will then proceed with a set of calculation that will ultimately increment our MD variables accordingly + the initial state of the MD variable (before operations).

The full code is available in the github and I will save you from the long lines, but conceptually it’s as below, not a Python code so do not copy paste, block[] is our 16 element word array:

# round 0 - we save the initial state of MD variables
AA = word_A
BB = word_B
CC = word_C
DD = word_D
# round 1
word_A=((word_A + F(word_B, word_C, word_D) + block[0]) % 2^32)<<3
word_A=((word_A + F(word_B, word_C, word_D) + block[4]) % 2^32)<<3
word_A=((word_A + F(word_B, word_C, word_D) + block[8]) % 2^32)<<3
word_A=((word_A + F(word_B, word_C, word_D) + block[12]) % 2^32)<<3
word_D=((word_D + F(word_A, word_B, word_C) + block[1]) % 2^32)<<7
word_D=((word_D + F(word_A, word_B, word_C) + block[5]) % 2^32)<<7
word_D=((word_D + F(word_A, word_B, word_C) + block[9]) % 2^32)<<7
word_D=((word_D + F(word_A, word_B, word_C) + block[13]) % 2^32)<<7
word_C=((word_C + F(word_D, word_A, word_B) + block[2]) % 2^32)<<11
word_C=((word_C + F(word_D, word_A, word_B) + block[6]) % 2^32)<<11
word_C=((word_C + F(word_D, word_A, word_B) + block[10]) % 2^32)<<11
word_C=((word_C + F(word_D, word_A, word_B) + block[14]) % 2^32)<<11
word_B=((word_B + F(word_C, word_D, word_A) + block[3]) % 2^32)<<19
word_B=((word_B + F(word_C, word_D, word_A) + block[7]) % 2^32)<<19
word_B=((word_B + F(word_C, word_D, word_A) + block[11]) % 2^32)<<19
word_B=((word_B + F(word_C, word_D, word_A) + block[15]) % 2^32)<<19
# round 2
word_A=((word_A + G(word_B, word_C, word_D) + block[0] + 0x5A827999
) % 2^32)<<3
word_A=((word_A + G(word_B, word_C, word_D) + block[1] + 0x5A827999
) % 2^32)<<3
word_A=((word_A + G(word_B, word_C, word_D) + block[2] + 0x5A827999
) % 2^32)<<3
word_A=((word_A + G(word_B, word_C, word_D) + block[3] + 0x5A827999
) % 2^32)<<3
word_D=((word_D + G(word_A, word_B, word_C) + block[4] + 0x5A827999
) % 2^32)<<5
word_D=((word_D + G(word_A, word_B, word_C) + block[5] + 0x5A827999
) % 2^32)<<5
word_D=((word_D + G(word_A, word_B, word_C) + block[6] + 0x5A827999
) % 2^32)<<5
word_D=((word_D + G(word_A, word_B, word_C) + block[7] + 0x5A827999
) % 2^32)<<5
word_C=((word_C + G(word_D, word_A, word_B) + block[8] + 0x5A827999
) % 2^32)<<9
word_C=((word_C + G(word_D, word_A, word_B) + block[9] + 0x5A827999
) % 2^32)<<9
word_C=((word_C + G(word_D, word_A, word_B) + block[10] + 0x5A827999
) % 2^32)<<9
word_C=((word_C + G(word_D, word_A, word_B) + block[11] + 0x5A827999
) % 2^32)<<9
word_B=((word_B + G(word_C, word_D, word_A) + block[12] + 0x5A827999
) % 2^32)<<13
word_B=((word_B + G(word_C, word_D, word_A) + block[13] + 0x5A827999
) % 2^32)<<13
word_B=((word_B + G(word_C, word_D, word_A) + block[14] + 0x5A827999
) % 2^32)<<13
word_B=((word_B + G(word_C, word_D, word_A) + block[15] + 0x5A827999
) % 2^32)<<13
# round 3
word_A=((word_A + H(word_B, word_C, word_D) + block[0] + 0x6ED9EBA1
) % 2^32)<<3
word_A=((word_A + H(word_B, word_C, word_D) + block[2] + 0x6ED9EBA1
) % 2^32)<<3
word_A=((word_A + H(word_B, word_C, word_D) + block[1] + 0x6ED9EBA1
) % 2^32)<<3
word_A=((word_A + H(word_B, word_C, word_D) + block[3] + 0x6ED9EBA1
) % 2^32)<<3
word_D=((word_D + H(word_A, word_B, word_C) + block[8] + 0x6ED9EBA1
) % 2^32)<<9
word_D=((word_D + H(word_A, word_B, word_C) + block[10] + 0x6ED9EBA1
) % 2^32)<<9
word_D=((word_D + H(word_A, word_B, word_C) + block[9] + 0x6ED9EBA1
) % 2^32)<<9
word_D=((word_D + H(word_A, word_B, word_C) + block[11] + 0x6ED9EBA1
) % 2^32)<<9
word_C=((word_C + H(word_D, word_A, word_B) + block[4] + 0x6ED9EBA1
) % 2^32)<<11
word_C=((word_C + H(word_D, word_A, word_B) + block[6] + 0x6ED9EBA1
) % 2^32)<<11
word_C=((word_C + H(word_D, word_A, word_B) + block[5] + 0x6ED9EBA1
) % 2^32)<<11
word_C=((word_C + H(word_D, word_A, word_B) + block[7] + 0x6ED9EBA1
) % 2^32)<<11
word_B=((word_B + H(word_C, word_D, word_A) + block[12] + 0x6ED9EBA1
) % 2^32)<<15
word_B=((word_B + H(word_C, word_D, word_A) + block[14] + 0x6ED9EBA1
) % 2^32)<<15
word_B=((word_B + H(word_C, word_D, word_A) + block[13] + 0x6ED9EBA1
) % 2^32)<<15
word_B=((word_B + H(word_C, word_D, word_A) + block[15] + 0x6ED9EBA1
) % 2^32)<<15
# add back the initial state
word_A = (word_A + AA) % 2^32
word_B = (word_B + BB) % 2^32
word_C = (word_C + CC) % 2^32
word_D = (word_D + DD) % 2^32

It’s a lengthy and not easy to ‘digest’ note but it shows the set of calculation that needs to happen in order to increment the MD variables accordingly.

Quick note about the two constants:

• Round 2, 0x5A827999 hexadecimal representation of square root of 2 (high order first)
• Round 3, 0x6ED9EBA1 hexadecimal representation of square root of 3 (high order first)

Once we get the final state of word_A/B/C/D (after having processed all the pass for each block) we can render the digest.

MD4 step 5— output

We need now to proceed for each 4 MD variables of 32 bits to decode it back into 4 bytes and then convert it into the hexadecimal rendering of the digest.

We can easily proceed as below:

md_digest = word_A.to_bytes(8, 'little')
md_digest += word_B.to_bytes(8, 'little')
md_digest += word_C.to_bytes(8, 'little')
md_digest += word_D.to_bytes(8, 'little')
print("".join(map(lambda x: hex(x).lstrip("0x"), md_digest)))

Conclusions

As per my previous MD2 tutorial, my implementation is not meant to be scalable or beautiful but to help understand the algorithm.

Remember, this algorithm has been proven unsafe, do not use it in critical applications.

Happy to reach out to further discuss if you have inputs, feedback nick@thecrypt.io

full code available here https://github.com/NickRHR/hashfunctions/blob/1c436187b2bcb18583a7da886e99406f36eec805/MD4/MD4_nfc.py